Skip to main content

Solving Binary Optimisation Problems using a Binary Genetic Algorithm 使用二元遺傳算法解決二元優化問題

Capital budgeting/project selection problem 資本預算/項目選擇問題​

  • A company is evaluating 4 projects which each run for 3 years and have the following characteristics. 一家公司正在評估 4 個項目，每個項目都運行 3 年，具有以下特徵。

    Capital requirements (££m)
    ProjectReturn ($m)Year123
    10.20.50.30.2
    20.31.00.80.2
    30.51.51.50.3
    40.10.10.40.1
    Available capital ($m)3.12.50.4

  • Decision problem: Which projects should be selected to maximize the total profits? 如何選擇項目以最大化總利潤？

Explanation: 解釋：

  • Once a project has been selected, all yearly capital requirement (investments) must be met in full 選擇項目後，必須全額滿足所有年度資本要求（投資）
  • There is a capital (budget) available for each year, that should not be exceeded 每年都有可用的資本（預算），不應超過

Problem formulation 問題公式化​

  • Decision variables x=[x1,x2,x3,x4]x = [x_1, x_2, x_3, x_4]: which project to select 決策變量x=[x1,x2,x3,x4]x = [x_1, x_2, x_3, x_4]：選擇哪個項目
    • x∈{0,1}x \in \{0, 1\}
    • xi=0x_i = 0: project ii is not selected
    • xi=1x_i = 1: project ii is selected
    • It is essentially a 0-1 (binary) integer programming problem
  • Objective: Maximize the expected returns 目標：最大化預期回報 maximise0.2x1+0.3x2+0.5x3+0.1x4maximise 0.2x_1 + 0.3x_2 + 0.5x_3 + 0.1x_4
  • Constraints: Yearly budget cannot be exceeded 年度預算不得超過 0:5x1+1:0x2+1:5x3+0:1x4<=3:10:5x1 + 1:0x2 + 1:5x3 + 0:1x4 <= 3:10:3x1+0:8x2+1:5x3+0:4x4<=2:50:3x1 + 0:8x2 + 1:5x3 + 0:4x4 <= 2:50:2x1+0:2x2+0:3x3+0:1x4<=0:40:2x1 + 0:2x2 + 0:3x3 + 0:1x4 <= 0:4
  • Question: The formulation above is a 0-1 integer programming problem. Do you think this kind of problems is easy to solve? Why? 上述公式化是一個 0-1 整數規劃問題。你認為這種問題是否容易解決？為什麼？

0-1 integer programming problems 0-1 整數規劃問題​

0-1 integer programming is NP-complete. See Richard Karp's 21 NP-complete problems

  • P vs NP vs NP-complete vs NP-hard
    • P: a complexity class that represents the set of all decision problems that can be solved in polynomial time (efficiently). P：一個複雜類，表示所有可以在多項式時間內解決的決策問題的集合。
    • NP: a complexity class that represents the set of all decision problems for which the instances where the answer is "yes" have proofs that can be verified in polynomial time. NP：一個複雜類，表示所有可以在多項式時間內解決的決策問題的集合。
    • NP-complete: NP-Complete is a complexity class which represents the set of all problems X in NP for which it is possible to reduce any other NP problem Y to X in polynomial time. NP-complete：NP-Complete 是一個複雜類，表示 NP 中所有問題 X 的集合，對於這些問題，可以在多項式時間內將任何其他 NP 問題 Y 簡化為 X。
      • Intuition: NP-complete means we can solve Y quickly if we know how to solve X quickly. NP-complete 意味著如果我們知道如何快速解決 X，則可以快速解決 Y。
  • P vs NP vs NP-complete vs NP-hard

How to solve the problem​

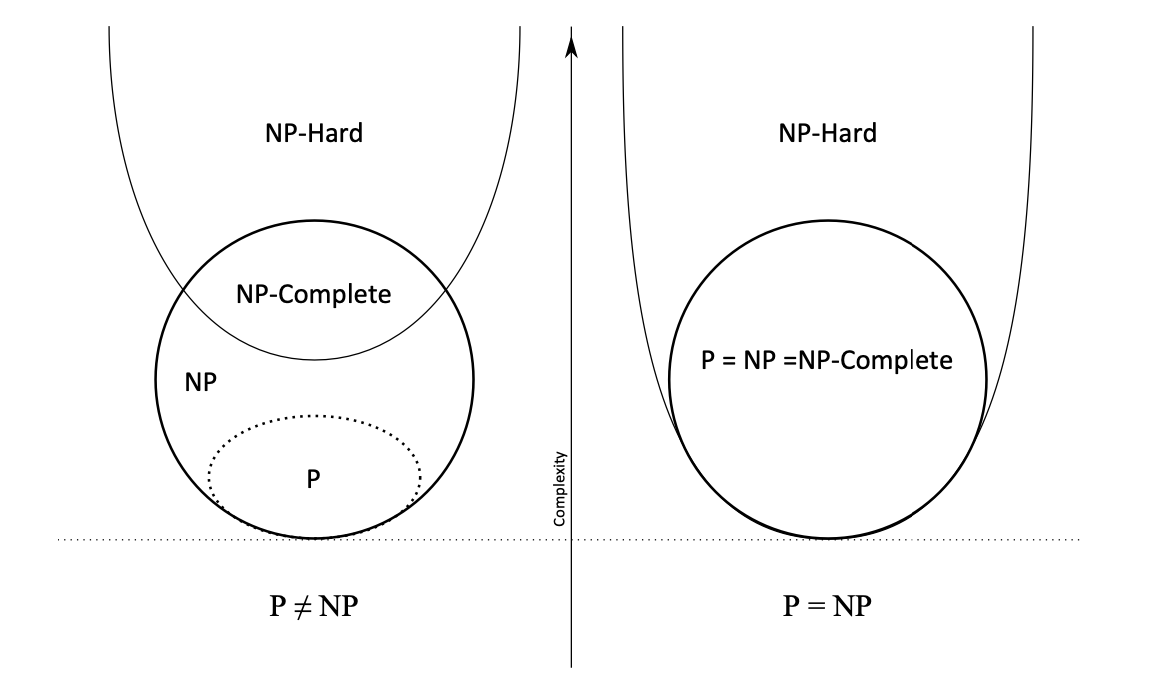
Figure 1: Euler diagram for P, NP, NP-complete, and NP-hard set of problems.

Figure 1: Euler diagram for P, NP, NP-complete, and NP-hard set of problems. From Wikipedia

  • Deterministic (Exact) methods:
    • The Branch & Bound Method: Relax the problem as a continuous problem 分支定界法：將問題放鬆為連續問題
  • Heuristic methods: 進化算法
    • Local search (hill climbing) 局部搜索（爬山）
    • Simulated Annealing (SA) 模擬退火
    • Genetic Algorithm (GA) 進化算法

Generic Evolutionary Algorithm 通用進化算法​

Building blocks of Evolutionary Algorithms 進化算法的構建塊​

  • An Evolutionary Algorithms consists of: 一個進化算法由以下組成：
    • representation: each solution is called an individual 表示：每個解決方案稱為一個個體
    • fitness (objective) function: to evaluate solutions 適應度（目標）函數：評估解決方案
    • variation operators: mutation and crossover 變異算子：突變和交叉
    • selection and reproduction : survival of the fittest 選擇和繁殖：適者生存

Genetic Representation: general principle 一般原則​

  • The selection of representation depends on the problem to be solved. 選擇表示取決於要解決的問題。
  • We have the following choices:
    • Binary representation 二進制表示
    • Real number representation 實數表示
    • Random key representation 隨機鍵表示
    • Other problem specific representations 其他特定問題的表示

Exercise: BGA for project selection problem 用 BGA 解決專案選擇問題​

  • Open my BGA_template.m file
  • Understand the fitness calculation function 理解適應度計算函數
  • Complete the following sections: 完成以下部分：
    • Initialisation 初始化
    • Crossover 交叉
    • Mutation 突變
  • Run you algorithm 30 times and record the average results and standard deviation. 重複運行 30 次，並記錄平均結果和標準差。

Exercise: Project selection problem extensions 專案選擇問題的擴展​

  • A new scenario: 一個新的情況：
    • If project 1 finishes in year 2, and all of the return from project 1 is available as capital in year 3 如果專案 1 在第 2 年完成，並且專案 1 的所有收益都在第 3 年作為資本可用
    • Projects 1 and 2 are mutually exclusive 專案 1 和 2 互斥
  • How to model this problem? 如何建模這個問題？

Exercise: Project selection problem extensions 專案選擇問題的擴展​

  • Solution:

    • If project 1 finishes in year 2, and all of the return from project 1 is available as capital in year 3, then this can be formulated by changing the capital requirement constraint for year 3 to: 如果專案 1 在第 2 年完成，並且專案 1 的所有收益都在第 3 年作為資本可用，則可以通過將第 3 年的資本需求約束更改為：

    0x1+0.2x2+0.3x3+0.1x4<=0.4+0.2x10x_1 + 0.2x_2 + 0.3x_3 + 0.1x_4 <=0.4 + 0.2x_1

    or equivalently: 或等價於：

    −0.2x1+0.2x2+0.3x3+0.1x4<=0.4-0.2x_1 + 0.2x_2 + 0.3x_3 + 0.1x_4 <= 0.4

    • However, we also need to change the objective function to count the return from the project. Question: How to do this? 然而，我們還需要更改目標函數以計算專案的收益。問題：如何做到這一點？
    • Projects 1 and 2 are mutually exclusive:

    x1+x2<=1x_1 + x_2 <= 1

  • Please read Prof. J E Beasley's OR-Notes on Integer Programming

Extra exercise​