Real-valued Coded Evolutionary Algorithms 實數編碼演化演算法

Arguments for using binary coding 使用二進制編碼的論據

• "The binary alphabet maximises the level of implicit parallelism" [1] 二進製字母表最大限度地提高了隱式並行性的水平

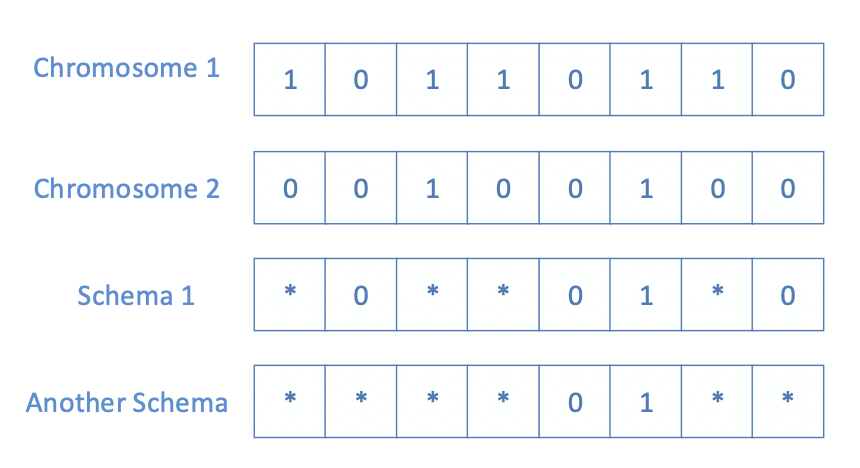
• 'Schema': a template that identities a subset of strings with similarities at certain string positions 識別在某些字符串位置具有相似性的字符串子集的模板

  

[1]: Goldberg, D.E. (1991c). Genetic and Evolutionary Algorithms Come of Age. Communication of the Association for Computing Machinery 37(3), 113–119.

Explanation of implicit parallelism 隱式並行性的解釋

• If a chromosome is of length $L$ then it contains $3^L$ schemata (as 3 possibilities, i.e., 0, 1 or $^*$ at each position) 如果染色體的長度為 $L$，則它包含 $3^L$ 模式（因為有 3 種可能性，即在每個位置上為 0、1 或 $^*$）
• For a population of $M$ individuals we are evaluating up to $M \cdot 3^L$ schemata 對於 $M$ 個人的人口，我們正在評估最多 $M \cdot 3^L$ 模式
• Some are fitter and some are weaker and some overlap with other schemata 有些更合適，有些更弱，有些與其他圖式重疊
• By selection, we can create a population that is full of fitter schemata 通過選擇，我們可以創建一個充滿擬合圖式的種群
• 'Implicit parallelism': we are not only evolving M individuals but also manipulating $M \cdot 3^L$ schemata 我們不僅在進化 M 個人，而且還在操作 $M \cdot 3^L$ 模式
• This essentially means that binary coding requires fewer strings to construct more schemata to sample larger search space 這本質上意味著二進制編碼需要更少的字符串來構建更多的圖式來採樣更大的搜索空間

Drawbacks of binary coding: Hamming cliff problem 二進制編碼的缺點：漢明懸崖問題

• Hamming cliff problem: one-bit mutation can make a large (or a small) jump; a multi-bit mutation can make a small (or large) jump. 一位突變可以使大（或小）跳躍；多位突變可以使小（或大）跳躍。

• Example:

  Genotype	000	001	010	011	100	101	110	111
  Phenotype	0	1	2	3	4	5	6	7

Solution to Hamming cliff problem 漢明懸崖問題的解決方案

• Solution: Gray encoding. For $a \in \{0, 1\}^L$ and $b \in \{0, 1\}^L$ where a is the standard binary encoded, and $b$ is Gray encoded, then 灰度編碼。對於 $a \in \{0, 1\}^L$ 和 $b \in \{0, 1\}^L$ 其中 a 是標準二進制編碼，$b$是格雷編碼，那麼

  $b_i= \begin{cases}a_i & \text { if } i=1 \\ a_{i-1} \oplus a_i & \text { if } i>1\end{cases}$

• Example:

  Binary encoded	000	001	010	011	100	101	110	111
  Gray encoded	000	001	011	010	110	111	101	100
  Phenotype	0	1	2	3	4	5	6	7

Drawbacks of binary coding 二進制編碼的缺點

• Problem in discrete search spaces: 離散搜索空間中的問題：

  • Redundancy problem: when the variables belongs to a nite discrete set with a cardinal dierent from a power of two, some binary strings are redundant, which correspond infeasible solutions 冗餘問題：當變量屬於基數與 2 的冪不同的有限離散集時，某些二進製字符串是冗餘的，對應於不可行的解決方案

  • Example: Suppose we have a combinatorial optimisation problem whose feasible set $A$ is $A = 0,2,3$, the cardinal of the set is $|A| = 3$ but we need a binary string of length of 2: 假設我們有一個組合優化問題，其可行集 $A$ 為 $A = 0,2,3$，該集的基數為 $|A| = 3$ 但我們需要一個長度為 2 的二進製字符串：

    Genotype	00	01	10	11
    Phenotype	0	1	2	3

• Problem in continuous search spaces: Precision 連續搜索空間中的問題：精度

  • Decoding function: 解碼功能

    • Divide $\vec{a} \in\{0,1\}^L$ into n segments of equal length $\vec{s}_i \in\{0,1\}^\frac{L}{n}$, $i = 1, ..., n$
    • Decode each segment into an integer $K_i, i = 1, ..., n$, and $K_i = \sum_{j=0}^{\frac{L}{n}} s_{i_j} \cdot 2^j$
    • Apply decoding function $h(K_i)$, i.e., map the integer linearly into the interval bound $xi \in [u_i, v_i]$:

  • The precision depends on L: might produce difficulties if the problem is large dimensional ($n$ is large) and requires great numerical precision are dealt with 如果問題是大維度的（$n$ 大）並且需要很大的數值精度，可能會產生困難

Real-valued vector representation 實數向量表示

• For continuous optimisation problems, real-valued vector representation is a natural way to represent solutions 實數向量表示是表示解決方案的自然方式
  • No dierences between genotypes and phenotypes: only a vector of real numbers called chromosome, e.g., $x = [x_1, x_2, ..., x_n] \in \mathbb{R}^n$ 基因型和表型之間沒有區別：只有一個稱為染色體的實數向量，例如，$x = [x_1, x_2, ..., x_n] \in \mathbb{R}^n$
  • Each gene in the chromosome represents a variable of the problem 染色體中的每個基因代表問題的一個變量
  • The precision is not restricted by the decoding/encoding functions 準確度不受解碼/編碼功能的限制
• Evolution Strategies, Evolutionary Programming and Differential 進化策略、進化規劃和微分
• Evolution are all based on real-valued vector representation 進化都是基於實值向量表示
• Advantages:
  • Simple, natural and faster: no need to encode and decode the solutions 簡單、自然並且更快：不需要編碼和解碼解決方案
  • Better precision and easy to handle large dimensional problems 更好的精度和較容易處理大維度問題

Real valued mutation 實數突變

• Randomly select a parent with probability $p_m \in [0,1]$ for mutation, and then randomly select a gene $c_i$ and apply mutation operator to it 隨機選擇一個具有概率 $p_m \in [0,1]$ 的父代進行突變，然後隨機選擇一個基因 $c_i$，並對其應用突變算子
• Real number mutation operators: 實數突變算子：
  • Uniform mutation 均勻突變
  • Non-uniform mutation 非均勻突變
  • Gaussian mutation 高斯突變

Real valued mutation: Uniform/Gaussian mutation 實數突變：均勻/高斯突變

• Uniform mutation: replace $c_i$ with a random (uniform) number $c_i^{\prime}$ generated from the interval bound of the variable $x_i \in [u_i, v_i]$ 均勻突變：用從變量 $x_i \in [u_i, v_i]$ 的區間邊界生成的隨機（均勻）數字 $c_i^{\prime}$ 替換 $c_i$

• Gaussian mutation: replace ci with ci0 which is calculated from: 高斯突變：用從計算出的 $c_{i}^{\prime}$ 替換 $c_i$

  $c_{i}^{\prime} = min(max(N(c_i, σ_i), u_i), v_i)$

  where $N(c_i, σ_i)$ is a Gaussian distribution with mean $c_i$ and standard deviation $σ_i$ which may depend on the length $l_i = v_i - u_i$ of the interval bound and typically $σ_i = \frac{1}{10}l_i$.

Real valued mutation: Non-uniform mutation 實數突變：非均勻突變

• Non-uniform mutation: replace $c_i$ with $c_{i}^{\prime}$ which is calculated from: 非均勻突變：用從計算出的 $c_{i}^{\prime}$ 替換 $c_i$

  $c_i^{\prime}= \begin{cases}c_i+\Delta\left(t, v_i-c_i\right) & \text { if } \tau \geq 0.5 \\ c_i-\Delta\left(t, c_i-u_i\right) & \text { if } \tau<0.5\end{cases}$

  where t is the number of current generation and $τ$ is a random number in the range of $[0, 1]$, and

  $\Delta(t, y)=y\left(1-r^{1-\frac{t}{g_m}}\right)^b$

  where r is a random number in the range of $[0,1]$, $g_m$ is the maximum number of generations and $b$ is a constant

• Question: what is the intuition of $\Delta(t,y)$

Real valued crossover 實數交叉

• Randomly select two parents $x_1=\{x_{1}^{[1]}, x_{2}^{[1]}, ..., x_{n}^{[1]}\}$ and $x_2=\{x_{1}^{[2]}, x_{2}^{[2]}, ..., x_{n}^{[2]}\}$ then apply a crossover operator to them 隨機選擇兩個父代 $x_1=\{x_{1}^{[1]}, x_{2}^{[1]}, ..., x_{n}^{[1]}\}$ 和 $x_2=\{x_{1}^{[2]}, x_{2}^{[2]}, ..., x_{n}^{[2]}\}$，然後對它們應用交叉算子

• Crossover operators: 交叉算子：

  • Flat crossover 平坦交叉
  • Simple crossover 簡單交叉
  • Whole arithmetical crossover 整體算術交叉
  • Local arithmetical crossover 本地算術交叉
  • Single arithmetical crossover 單一算術交叉
  • BLX-$\alpha$ crossover BLX-$\alpha$ 交叉

Real valued crossover operators 實數交叉算子

• Flat crossover: One offspring, $h = \{h_1, h_2, ..., h_n\}$, is generated, where $h_i$ is a randomly (uniformly) chosen value in the interval $[x_{i}^{[1]}, x_{i}^{[2]}]$ if $x_{i}^{[1]} < x_{i}^{[2]}$ or $[x_{i}^{[2]}, x_{i}^{[1]}]$ if $x_{i}^{[2]} < x_{i}^{[1]}$ 平坦交叉：生成一個後代 $h = \{h_1, h_2, ..., h_n\}$，其中 $h_i$ 是在區間 $[x_{i}^{[1]}, x_{i}^{[2]}]$ 中隨機（均勻）選擇的值，如果 $x_{i}^{[1]} < x_{i}^{[2]}$ 或 $[x_{i}^{[2]}, x_{i}^{[1]}]$，如果 $x_{i}^{[2]} < x_{i}^{[1]}$

• Simple crossover: a crossover point $i \in \{1, ..., n\}$ is randomly chosen, and the variables beyond this point are swap to create two new offspring: 簡單交叉：隨機選擇一個交叉點 $i \in \{1, ..., n\}$$，然後交換這個點之後的變量，以創建兩個新的後代：

  $h_1 = \{x_{1}^{[1]}, x_{2}^{[1]}, ..., x_{i-1}^{[1]}, x_{i}^{[2]}, x_{i+1}^{[2]}, ..., x_{n}^{[2]}\}$ $h_2 = \{x_{1}^{[2]}, x_{2}^{[2]}, ..., x_{i-1}^{[2]}, x_{i}^{[1]}, x_{i+1}^{[1]}, ..., x_{n}^{[1]}\}$

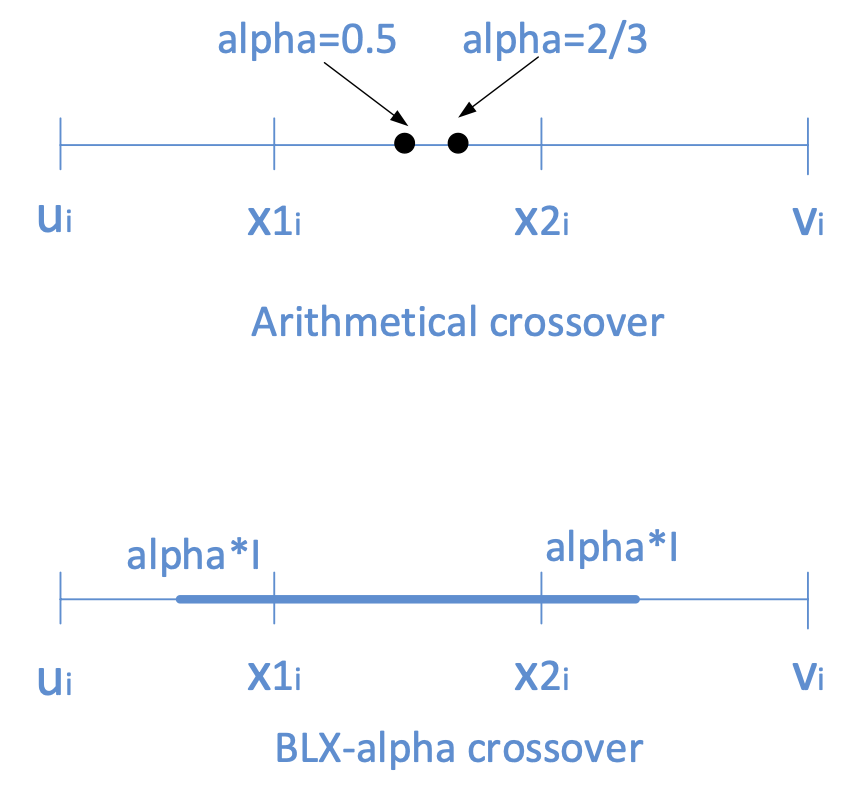
• Whole arithmetical crossover: two offspring $h_k = \{h_1^k, h_2^k, ..., h_n^k\}$, $k = 1,2$ are generated, where $h_i^{[1]} = \alpha x_n^{[1]} + (1-\alpha)x_i^{[2]}$ and and parameter is a random number in the range of $[0,1]$ 整體算術交叉：生成兩個後代 $h_k = \{h_1^k, h_2^k, ..., h_n^k\}$，$k = 1,2$，其中 $h_i^{[1]} = \alpha x_n^{[1]} + (1-\alpha)x_i^{[2]}$，參數是區間 $[0,1]$ 中的隨機數

• Local arithmetical crossover: the same as whole arithmetic crossover, except $\alpha \in \mathbb{R}^n$ is a vector of which each element is random number in the range of $[0,1]$ 本地算術交叉：與整體算術交叉相同，除了 $\alpha \in \mathbb{R}^n$ 是一個向量，其中每個元素是區間 $[0,1]$ 中的隨機數

• Single arithmetical crossover: choose a gene and then replace it with the arithmetic average of genes at the position of two parents, other genes are copied from the parents. 單一算術交叉：選擇一個基因，然後用兩個父代的位置的基因的算術平均值替換它，其他基因從父代複製。

• BLX-$\alpha$ crossover: an offspring is generated: $h=\{h_1, h_2, ..., h_n\}$, where $h_i$ is a randomly (uniformly) generated number of the interval $[h_{min} - l \cdot \alpha, h_{max} + l \cdot \alpha], h_{max} = max(x_i^{[1]}, x_i^{[2]}), h_min = min(x_i^{[1]}, x_i^{[2]})$ and $l = h_{max} - h_{min}$ 生成一個後代 $h=\{h_1, h_2, ..., h_n\}$，其中 $h_i$ 是區間 $[h_{min} - l \cdot \alpha, h_{max} + l \cdot \alpha]$ 中隨機（均勻）生成的數字，$h_{max} = max(x_i^{[1]}, x_i^{[2]}), h_min = min(x_i^{[1]}, x_i^{[2]})$，$l = h_{max} - h_{min}$

Examples

Conclusion 結論

• Binary coded GAs, despite its biological plausibility, are not ideal for a lot of problems 二進制編碼的遺傳算法儘管具有生物學上的合理性，但對於許多問題來說並不理想
• Real valued representation is the most natural way for continuous optimisation problems 實數表示是連續最佳化問題的最自然的方式
• Variation operators for real-valued coded GAs are also mutations and crossover 實值編碼 GA 的變異算子也是突變和交叉

Reading list

• Z. Michalewicz, Genetic Algorithms + Data Structures = Evolution Programs, 1996
• T. Baeck, D. B. Fogel, and Z. Michalewicz, Handbook on Evolutionary Computation, 1997