Selection and Reproduction 選擇與繁殖

Generic Evolutionary Algorithm 通用進化算法

$X_0$ := generate initial population of solutions
terminationflag := false
t := 0
Evaluate the fitness of each individual in $X_0$.
while (terminationflag != true)
  Selection: Select parents from $X_t$ based on their fitness.
  Variation: Breed new individuals by applying variation operators to parents Fitness calculation: Evaluate the fitness of new individuals. Reproduction: Generate population $X_{t+1}$ by replacing least-fit individuals
  t := t + 1
  If a termination criterion is met: terminationflag := true
Output $x_best$

Selection 選擇

• Selection is not a search operator but influences search performance significantly 選擇不是搜索運算符，但會顯著影響搜索性能

• Selection usually is performed before variation operators: selects better fit individuals for breeding 選擇通常在變異算子之前進行：選擇更適合的個體進行育種

• Selection: emphasises on exploiting better solutions in a population: 強調在群體中開發更好的解決方案：

  • Select one or more copies of good solutions. 選擇一份或多份好的解決方案。
  • Inferior solutions will be selected but with a much less chance 將選擇較差的解決方案，但機會要小得多

• Question: Why we still select those inferior solutions? 為什麼我們仍然選擇那些劣質的解決方案？

Selection Schemes 選擇方案

• Fitness Proportional Selection (FPS) 適應度比例選擇
• Ranking Selection 排名選擇
• Truncation Selection 截斷選擇
• Tournament Selection 比賽選擇
• $(μ + λ)$ and $(μ, λ)$ selection

Fitness Proportional Selection 適應度比例選擇

• Fitness Proportional Selection (FPS) 適應度比例選擇 = Roulette Wheel Selection 輪盤選擇

• Selecting individuals $i$ with a probability: 選擇個體 $i$ 的概率為：

  $P(i) = \frac{f_i}{\sum_{j=1}^N f_j}$

  where $f_i$ is the fitness of individual $i$ and $N$ is the population size. 其中 $f_i$ 是個體 $i$ 的適應度，$N$ 是群體大小。

• Does not allow negative fitness values. 不允許負的適應度值。

• Individual with higher fitness will be less likely to be eliminated, but still a chance that they may be (Discuss later). 適應度較高的個體不太可能被淘汰，但仍有機會被淘汰（稍後討論）。

• Individual with low fitness values may survive the selection process: allows some weak individuals who may help escaping from local optima. 適應度較低的個體可能會在選擇過程中存活下來：允許一些弱的個體，這些個體可能有助於逃離局部最優解。

Fitness Proportional Selection: scaling 適應度比例選擇：縮放

• Observation: in early generations, there might be a domination of "super individuals" with very high fitness values 在早期代，可能會有一些"超級個體"擁有非常高的適應度值

• Question: what problems will "super individuals" cause in EAs? 什麼問題會導致"超級個體"在 EAs 中產生？

• Observation: In later generations, there might be no much separation among individuals 在後代，個體之間可能沒有太多的分離

• Question: What are the problems in EAs with no much separation among individuals? 在沒有太多分離的 EAs 中有什麼問題？

• Problems:

  • Question: what problems will "super individuals" cause in EAs? 什麼問題會導致"超級個體"在 EAs 中產生？
  • Answer: Premature convergence to a local optimum 早期收斂到局部最優解
  • Question: What problems will caused in EAs with no much separation among individuals? 在沒有太多分離的 EAs 中有什麼問題？
  • Answer: Slow convergence 慢速收斂

• Question: How to maintain the same selection pressure throughout the run? 如何在運行過程中維持相同的選擇壓力？

• Solution: replace raw fitness values $f_{i}$ with a scaled fitness value $f_{i}^{\prime}$ 用縮放的適應度值 $f_{i}^{\prime}$ 代替原始的適應度值 $f_{i}$

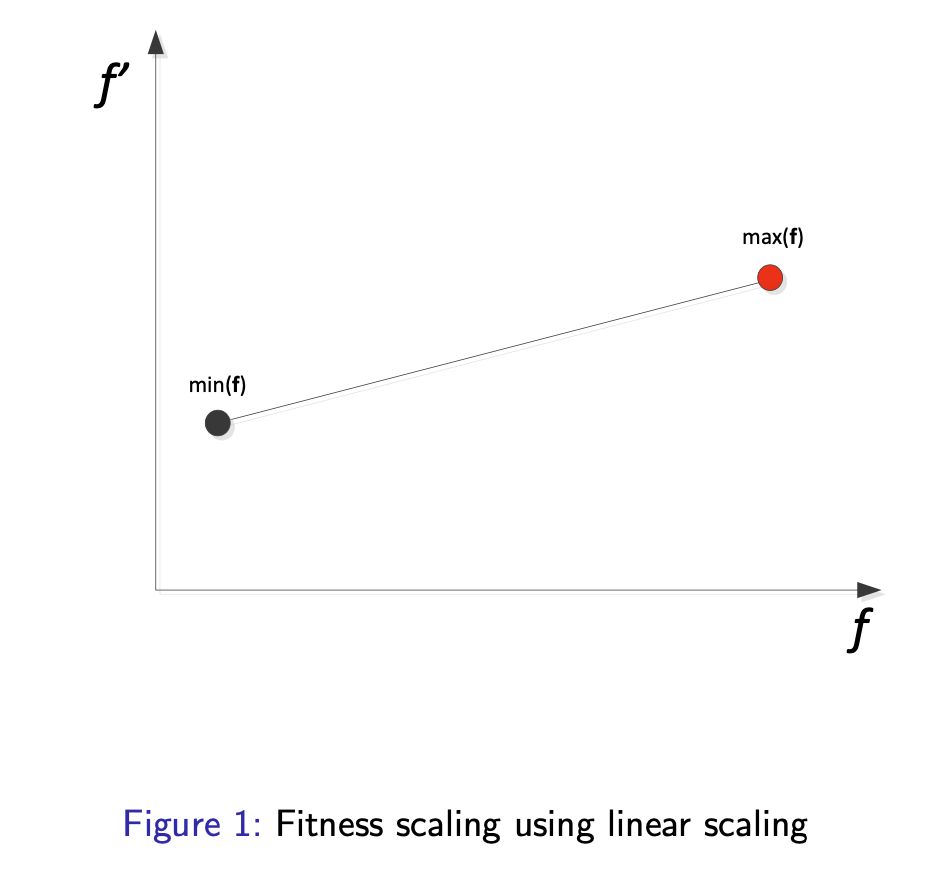
• Linear scaling:

  $$ f_i^{\prime}=a+b \cdot f_i $$

  where a and b are constants, usually set as $a = max(f)$ and $b = min(f)/M < 1$, where $f = f1,f2,··· ,M$

  

Ranking Selection 排名選擇

• Sort population size of M from best to worst according to their fitness values: 根據適應度值將群體大小為 M 的個體從最好到最差進行排序：

  $$ x{(M-1)}^{\prime}, x{(M-2)}^{\prime}, x{(M-3)}^{\prime}, \cdots, x{(0)}^{\prime} $$

• Select the top $γ$-ranked individual $x_{γ}^{\prime}$ with probability $p(γ)$, where $p(γ)$ is a ranking function, e.g.

  • linear ranking
  • exponential ranking
  • power ranking
  • geometric ranking

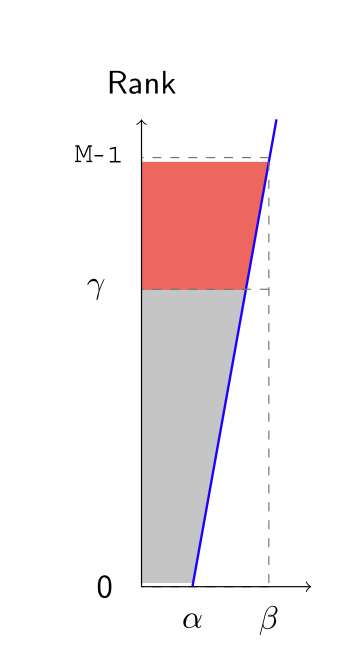
Linear Ranking Function 線性排名函數

• Linear ranking function:

  $p(\gamma)=\frac{\alpha+(\beta-\alpha) \cdot \frac{\gamma}{M-1}}{M}$

  where implies $\alpha + \beta = 2$ and 1 ≤ $\beta$ ≤ 2

• In expectation

  • Best individual, i.e., $γ = M - 1$, reproduced $\beta$ times: $p(M-1) = \frac{\beta}{M}$.
  • Worst individual, i.e., $γ = 0$, reproduced $\alpha$ times: $p(0) = \frac{\alpha}{M}$.

• Question: how to set $\alpha$ and $\beta$ to make EA behave like a random search algorithm?

Other Ranking Functions 其他排名選擇函數

Give you different, usually non-linear relationships between the rank γ and the selection probability $p(γ)$:

• Power ranking function:

  $p(\gamma)=\frac{\alpha+(\beta - \alpha) \cdot \left(\frac{\gamma}{M-1}\right)^k}{C}$

• Geometric ranking function:

  $p(\gamma)=\frac{\alpha \cdot (1 - \alpha)^{M-1-\gamma}}{C}$

• Exponential ranking function:

  $p(\gamma)=\frac{1-e^{-\gamma}}{C}$

  where $C$ is a normalising factor and $0<\alpha<\beta$.

Truncation Selection 截斷選擇

• Steps:
  • Rank individuals by fitness values
  • Select some proportion, $k$, (e.g. $k = \frac{1}{2}$), of the top ranked individuals
• Usually, k = 0.5 (top 50%) or k = 0.3 (top 30%)
• Can be seen as the simplest, deterministic ranking selection

Tournament Selection 比賽選擇

• Tournament selection with tournament size k:
  • Step 1: Randomly sample a subset $P\prime$ of k individuals from population $P$
  • Step 2: Select the individual in $P\prime$ with highest fitness Repeat Steps 1 and 2 until enough offspring are created
• Among the most popular selection methods in genetic algorithms
• Binary tournament selection $(k = 2)$ is the most popular one

$(μ + λ)$ and $(μ, λ)$ selection

• First proposed in Evolution Strategies. 首先在演化策略中提出。
• $(μ + λ)$ selection:
  • Parent population of size $μ$
  • Generate $λ$ offspring from randomly chosen parents
  • Next population is $μ$ best individuals among parents and offspring
• $(μ, λ)$ selection where $λ > μ$
  • Parent population of size $μ$
  • Generate $λ$ offspring from randomly chosen parents
  • Next population is $μ$ best individuals among offspring

Selection Pressure 選擇壓力

• Selection pressure: degree to which selection emphasises on the better individuals. 選擇壓力：選擇強調優秀個體的程度。
• Question 1: How does selection pressure affect the balance between exploitation and exploration? 選擇壓力如何影響探索和開發之間的平衡？
• Answer 1:
  • Higher selection pressure → exploitation → fast convergence to local optimum, e.g., premature
  • Low selection pressure → exploration → slow convergence
• Question 2: Given an EA with a selection scheme, how will you measure selection pressure? 給定一個具有選擇方案的 EA，如何衡量選擇壓力？
• Answer 2: Take-over time $τ^∗$ [1]:
  • Let's assume population size is M and initial population with one unique fittest individual $x^{∗}$
  • Apply selection repeatedly with no other operators.
  • $τ^∗$ is number of generations until population consists of $x^{∗}$ only.
• Higher take-over time means lower selection pressure.

[1]: Goldberg, D. E. and Deb, K. (1991). A comparative analysis of selection schemes used in genetic algorithms. In Foundations of Genetic Algorithms. Morgan Kaufmann.

Selection function	τ∗ ≈	Note
Fitness prop.	$\frac{M ln M}{c}$	Assuming a power law objective function f (x) = xc
Linear ranking	$\frac{2ln(M-1)}{\beta-1}$	1≤β≤2
Truncation	$ln M$
Tournament	$\frac{M}{k}$	tournament size $k$
$(μ+λ)$	$\frac{lnλ}{ln(\frac{λ}{μ})}$

Reproduction 繁殖

• Reproduction: to control how genetic algorithm creates the next generation 繁殖：控制遺傳演算法如何創建下一代

• Generational vs Steady state 世代 vs 穩態

  • Generational EAs: also called standard EAs, use all new individuals after variations to replace the worse individuals in the old population to create a new population (then selection) 世代式 EA：也稱為標準 EA，在變異後使用所有新個體來取代舊世代中較差的個體以創建新世代（然後選擇）
  • Steady state EAs: only use a few or even one single new individual to replace the old population at any one time 堅定狀態 EA：只在任何一個時間點使用一些甚至一個新個體來取代舊世代

• n-Elitisms: always copy the N best individuals to the next generation n-Elitisms：總是將 N 個最好的個體複製到下一代

• Generational gap: the overlap (i.e., individuals that did not go through any variation operators) between the old and new generations. 世代間隙：舊世代和新世代之間的重疊（即沒有經過任何變異運算子的個體）。

Conclusion 結論

• Selection and reproduction are two important ingredients of EAs 選擇和復制是 EA 的兩個重要組成部分
• The major difference between selection methods is based on: 選擇方法之間的主要差異在於：
  • Relative fitness: fitness proportional selection 相對適應度：適應度比例選擇
  • Ranking: tournament, truncation, (μ + λ) and (μ, λ) 排名：比賽，截斷，（μ + λ）和（μ，λ）
• Takeover time: quantitative measure of selection pressure 接管時間：選擇壓力的定量衡量
• Selection pressure is used to control the balance between exploitation and exploration: 選擇壓力用於控制探索和開發之間的平衡：
  • Higher selection pressure → exploitation → fast convergence to local optimum, e.g., premature 更高的選擇壓力 → 利用 → 快速收斂到局部最優，例如，過早
  • Low selection pressure → exploration → slow convergence 低選擇壓力 → 探索 → 慢速收斂