Skip to main content

Face Recognition 人臉識別

Eigenfaces: the idea 特徵臉：想法​

  • Think of a face as being a weighted combination of some "component" or "basis" faces 將面孔視為某 ​​ 些"組件"或"基礎"面孔的加權組合
  • These basis faces are called eigenfaces 這些基礎面孔稱為特徵面孔

1

Eigenfaces: representing faces 特徵臉：表示臉​

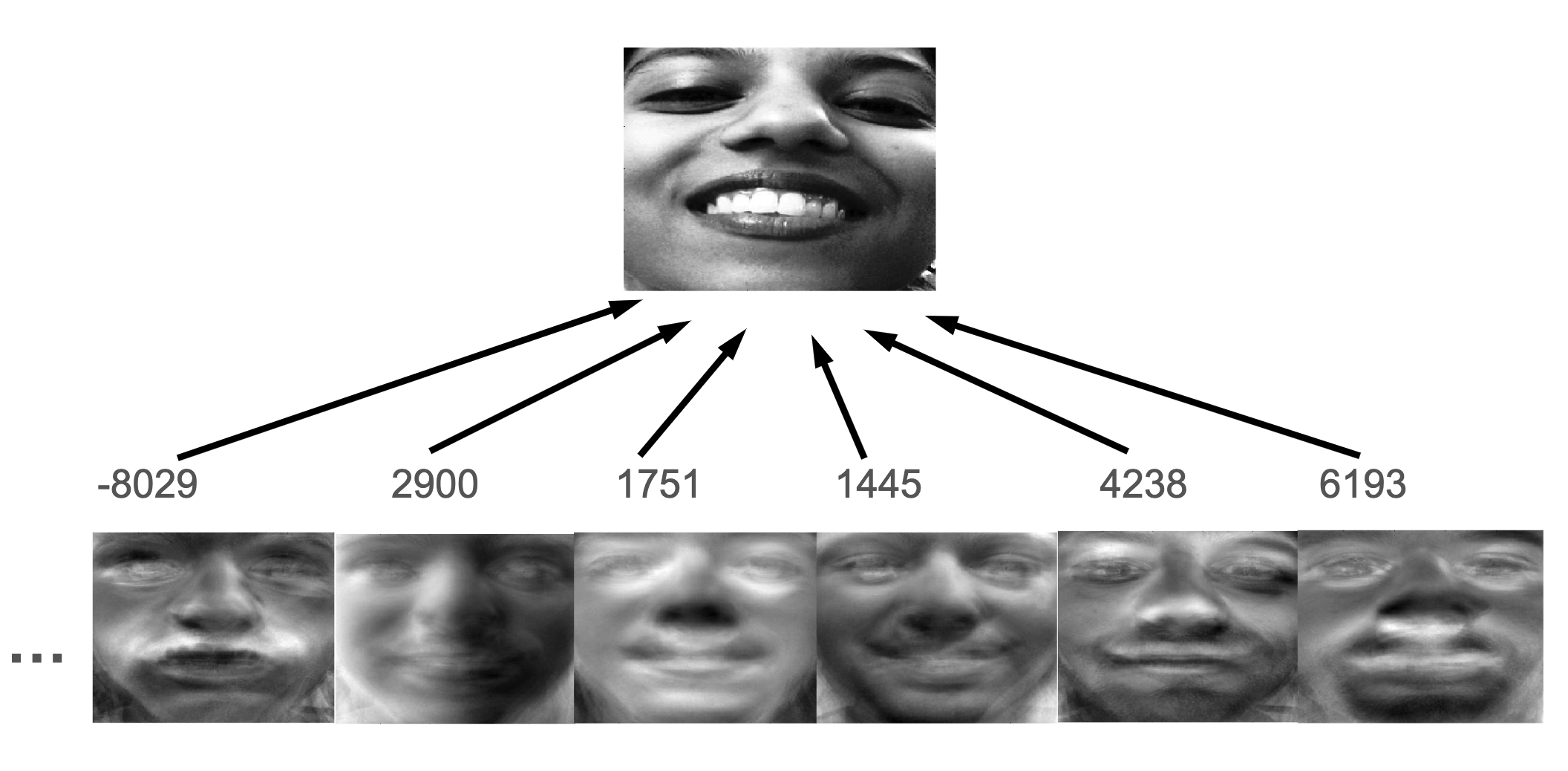
  • These basis faces can be differently weighted to represent any face 這些基礎面孔可以有不同的權重來代表任何面孔
  • So we can use different vectors of weights to represent different faces 我們可以使用不同的權重向量來表示不同的面孔

2

Learning Eigenfaces 學習特徵臉​

Q: How do we pick the set of basis faces? 如何選擇一組基礎面孔？

A: We take a set of real training faces 我們拿一組真實的訓練面孔

3

Then we find (learn) a set of basis faces which best represent the differences between them 我們找到（學習）一組基礎面孔，最好代表他們之間的差異

We'll use a statistical criterion for measuring this notion of "best representation of the differences between the training faces" 我們將使用統計標準來衡量"最佳表示訓練面孔之間的差異"的這一概念

We can then store each face as a set of weights for those basis faces 我們可以將每個面孔存儲為這些基礎面孔的一組權重

Using Eigenfaces: recognition & reconstruction 使用特徵臉：識別和重建​

  • We can use the eigenfaces in two ways 我們可以用兩種方式使用特徵面孔

  • 1: we can store and then reconstruct a face from a set of weights 我們可以存儲然後從一組權重重建一個面孔

    4

  • 2: we can recognise a new picture of a familiar face by comparing it to the stored weights 我們可以通過將其與存儲的權重進行比較來識別一個新的熟悉面孔的圖片

    5

Learning Eigenfaces 學習特徵臉​

  • How do we learn them? 如何學習它們？
  • We use a method called Principle Components Analysis (PCA) 我們使用一種稱為主成分分析（PCA）的方法
  • To understand this we will need to understand 要理解這一點，我們需要理解
    • What an eigenvector is 什麼是特徵向量
    • What covariance is 什麼是協方差
    • what is happening in PCA qualitatively 什麼是在 PCA 中發生的事情

Eigenfaces in detail 特徵臉的細節​

  • All we are doing in the face case is treating the face as a point in a high- dimensional space, and then treating the training set of face pictures as our set of points 我們在面孔案例中所做的所有事情都是將面孔視為高維空間中的一個點，然後將訓練集中的面孔圖片視為我們的一組點
  • To train: 我們要訓練：
    • Take your images, and re-arrange as a 2Dmatrix 拍攝您的圖像，並重新排列為二維矩陣
      • Rows: Each image 行：每個圖像
      • Columns: Each pixel value 列：每個像素值
    • We calculate the covariance matrix of the faces 我們計算面孔的協方差矩陣
    • We then find the eigenvectors of that covariance matrix 我們然後找到該協方差矩陣的特徵向量
  • These eigenvectors are the eigenfaces or basis faces 這些特徵向量是特徵面孔或基礎面孔
  • Eigenfaces with bigger eigenvalues will explain more of the variation in the set of faces, i.e. will be more distinguishing 特徵面孔的特徵值越大，說明面孔集中的變化越多，即將更具有區分性

Eigenfaces: image space to face space 特徵臉：圖像空間到面孔空間​

  • When we see an image of a face we can transform it to face space 我們看到一個面孔的圖像時，我們可以將其轉換為面孔空間
    wk=xi⋅vk\mathbf{w}_k=\mathbf{x}^{\mathbf{i}} \cdot v_k
  • There are k=1...n eigenfaces vkv_k
  • The ithface in image space is a vector xix^i
  • The corresponding weight is wkw_k
  • We calculate the corresponding weight for every eigenface 我們計算每個特徵臉對應的權重

6

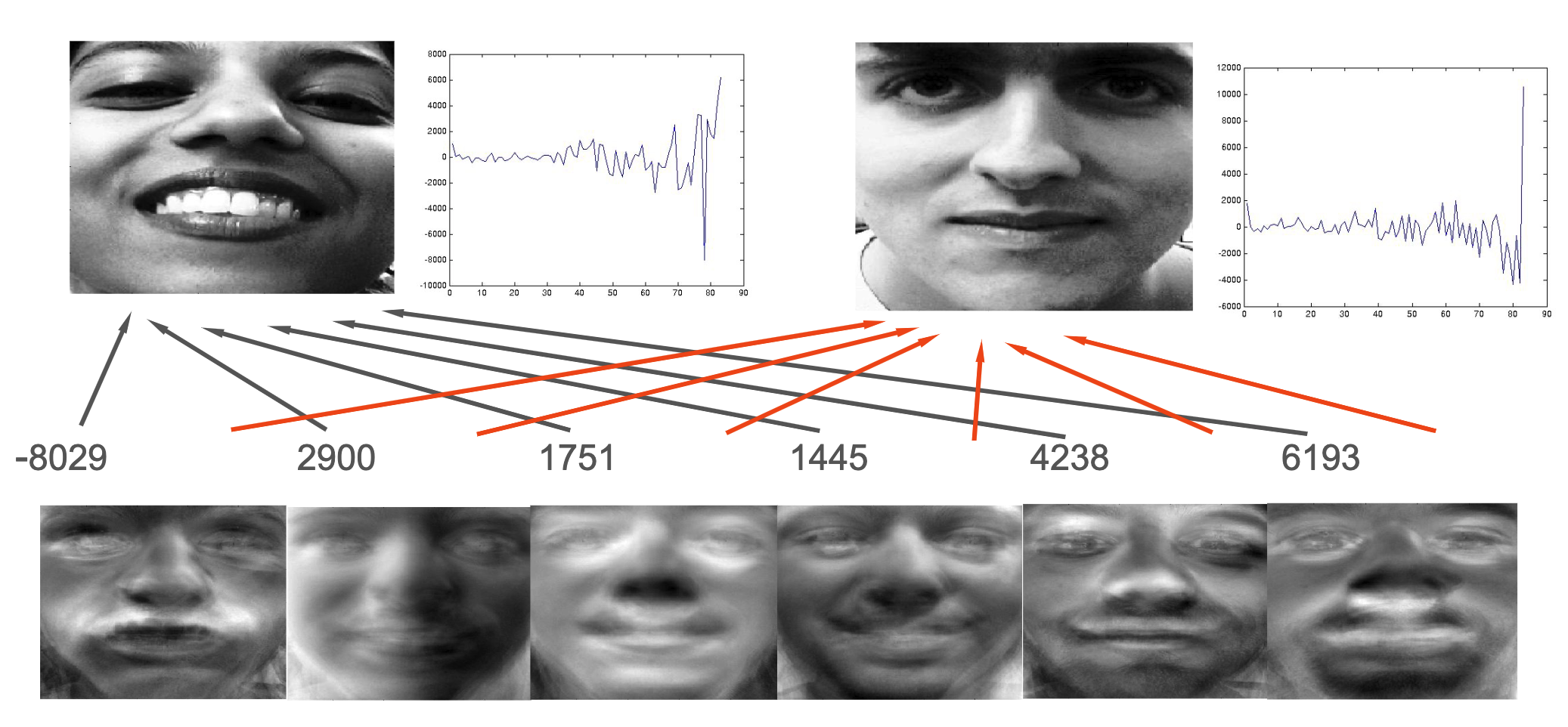
Recognition in face space 面孔空間中的識別​

  • Recognition is now simple. We find the euclidean distance d between our face and all the other stored faces in face space: 識別現在很簡單。我們找到我們的面孔與面孔空間中所有其他存儲的面孔之間的歐幾里得距離 d：
    d(w1,w2)=∑i=1n(wi1−wi2)2d\left(w^1, w^2\right)=\sqrt{\sum_{i=1}^n\left(w_i^1-w_i^2\right)^2}
  • The closest face in face space is the chosen match 最接近的面孔在面孔空間中是選定的匹配

7

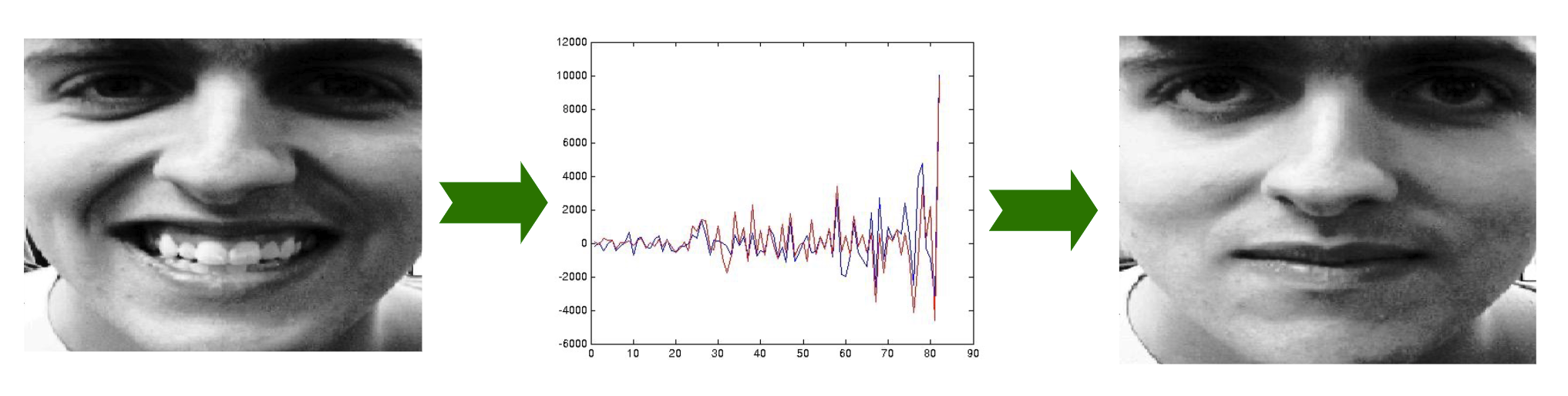
Reconstruction in face space 面孔空間中的重建​

  • The more eigenfaces you have the better the reconstruction, but you can have high quality reconstruction even with a small number of eigenfaces 你有越多的特徵面孔，重建就越好，但即使使用少數特徵面孔，你也可以有高質量的重建

8

Summary 总结​

  • Statistical approach to visual recognition 統計方法用於視覺識別
  • Also used for object recognition and tracking 也用於物體識別和跟蹤
  • Problems 問題
  • Reference: M. Turk and A. Pentland (1991). Eigenfaces for recognition, Journal of Cognitive Neuroscience , 3(1): 71–86.