Skip to main content

Hough Transform 霍夫轉換

The story so far 目前為止的故事​

  • We know how to find edges by convolving with the derivative of a Gaussian filter in two directions 我們知道如何通過在兩個方向上與高斯濾波器的導數進行卷積來找到邊緣
  • Steps:
    • Take image 拿圖片
    • Convolve mask with image for each direction 對每個方向將掩模與圖像進行卷積
      • Calculate derivatives Gx and Gy 計算導數 Gx 和 Gy
    • Calculate magnitude = M(G⃗)=Gx2+Gy2M(\vec{G})=\sqrt{G_x^2+G_y^2} 計算大小= M(G⃗)=Gx2+Gy2M(\vec{G})=\sqrt{G_x^2+G_y^2}

1

Finding edge features 找到邊緣特徵​

But we haven't found edge segments, only edge points 但我們還沒有找到邊緣段，只找到了邊緣點

How can we find and describe more complex features? 我們如何找到和描述更複雜的特徵？

The Hough transform is a common approach to finding parameterised line segments (here straight lines) 霍夫轉換是一種常見的方法，用於找到參數化的線段（這裡是直線）

2

The basic idea 基本思想​

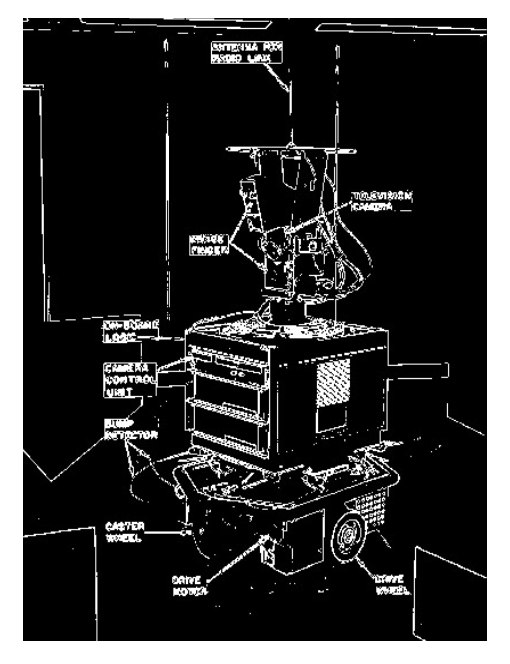
Each straight line in this image can be described by an equation 這個圖像中的每條直線都可以用一個方程式來描述

Each white point if considered in isolation could lie on an infinite number of straight lines 如果單獨考慮每個白點，它可以在無限多條直線上

3

The basic idea 基本思想​

Each straight line in this image can be described by an equation 這個圖像中的每條直線都可以用一個方程式來描述

Each white point if considered in isolation could lie on an infinite number of straight lines 如果單獨考慮每個白點，它可以在無限多條直線上

In the Hough transform each point votes for every line it could be on 在霍夫轉換中，每個點都為它可能在的每條直線投票

The lines with the most votes win 得票最多的線贏了

4

How do we represent lines? 我們如何表示線？​

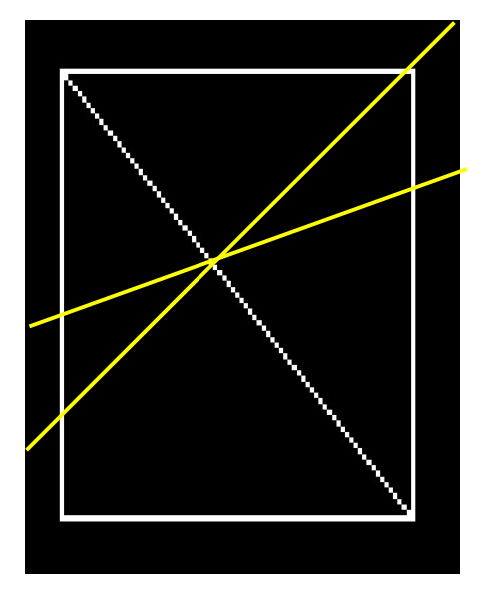
Any line can be represented by two numbers 任何線都可以用兩個數字來表示

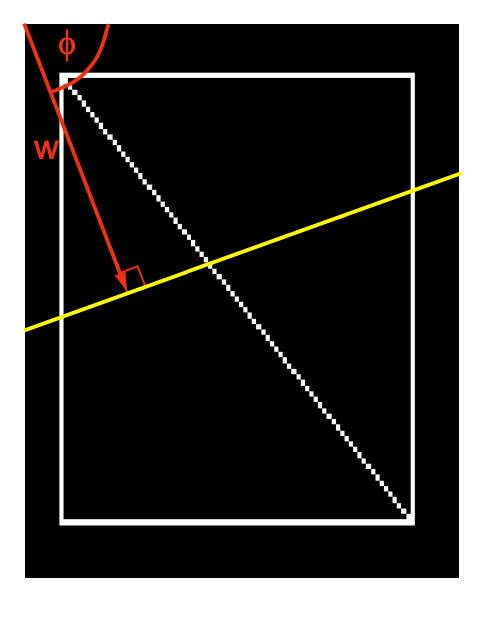
Here we will represent the yellow line by (w,f) 在這裡，我們將用 (w,f) 來表示黃色線

In other words we define it using 也就是說，我們用它來定義

  • a line from an agreed origin 一條從同意的起點開始的線
  • of length w 長度為 w
  • at angle ϕ\phi to the horizontal 在水平線上的角度 ϕ\phi

5

Hough space 霍夫空間​

Since we can use (w,f) to represent any line in the image space 由於我們可以使用 (w,f) 來表示圖像空間中的任何線

We can represent any line in the image space as a point in the plane defined by (w,f) 我們可以將圖像空間中的任何線表示為由 (w,f) 定義的平面中的一個點

This is called Hough space 這被稱為霍夫空間

6

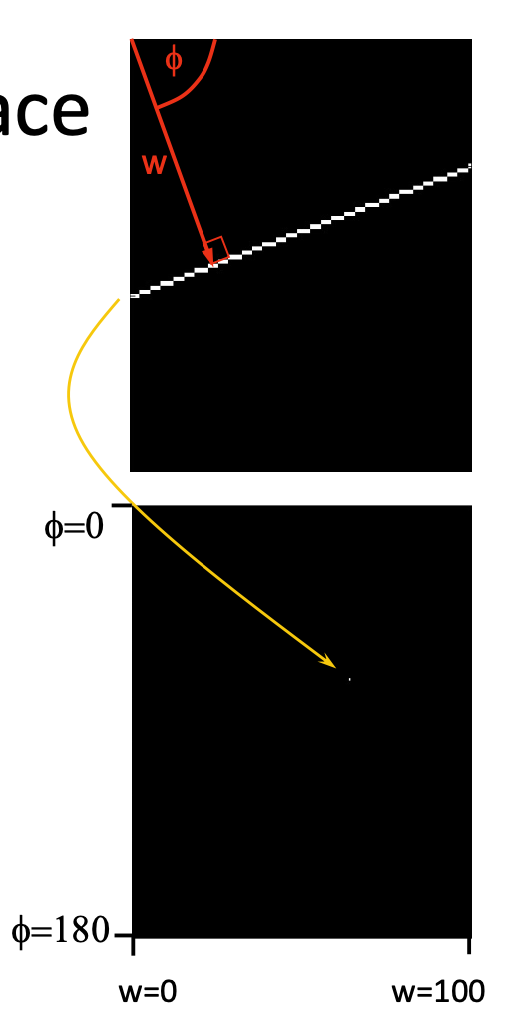
How does a point in image space vote? 圖像空間中的一個點如何投票？​

w = x cos(f) + y sin(f)

7

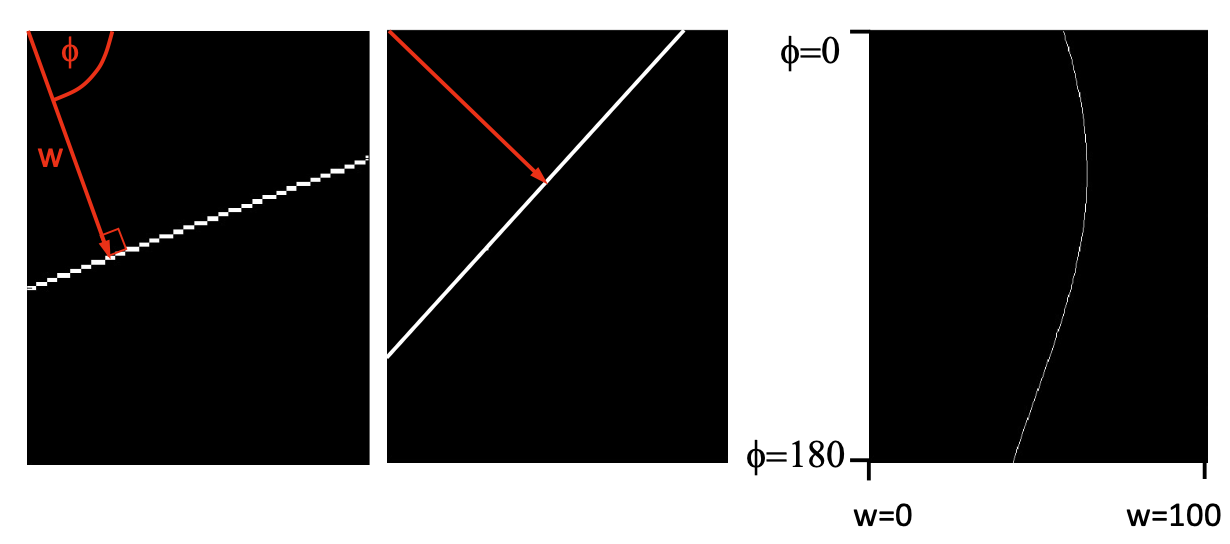
How do multiple points prefer one line? 多個點如何偏好一條線？​

One point in image space corresponds to a sinusoidal curve in houghspace 圖像空間中的一個點對應於霍夫空間中的一個正弦曲線

Two points correspond to two curves in Hough space 兩個點對應於霍夫空間中的兩條曲線

The intersection of those two curves has "two votes". 這兩條曲線的交點有"兩個投票"。

This intersection represents the straight line in image space that passes through both points 這個交點代表通過兩個點的圖像空間中的直線

8

Hough Transform 霍夫轉換​

9

A simple example of Hough Transform 霍夫轉換的一個簡單例子​

10

11

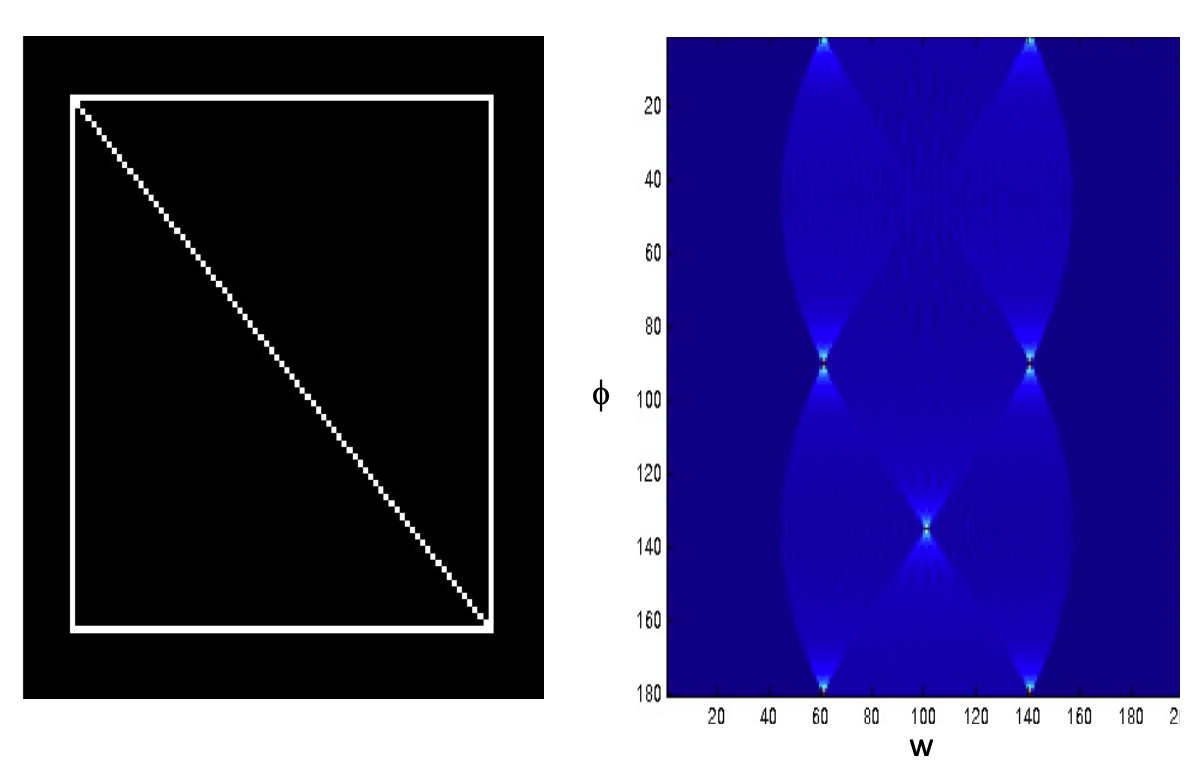
Hough Transform 霍夫轉換​

  • There are generalised versions for ellipses, circles 有一般化版本的橢圓，圓
  • For the straight line transform we need to supress non-local maxima in the accumulator 對於直線轉換，我們需要在累加器中抑制非局部最大值
  • The input image could also benefit from edge thinning 輸入圖像也可以從邊緣瘦身中受益
  • Single line segments not isolated 單線段未隔離
  • Will still fail in the face of certain textures 單線段未隔離

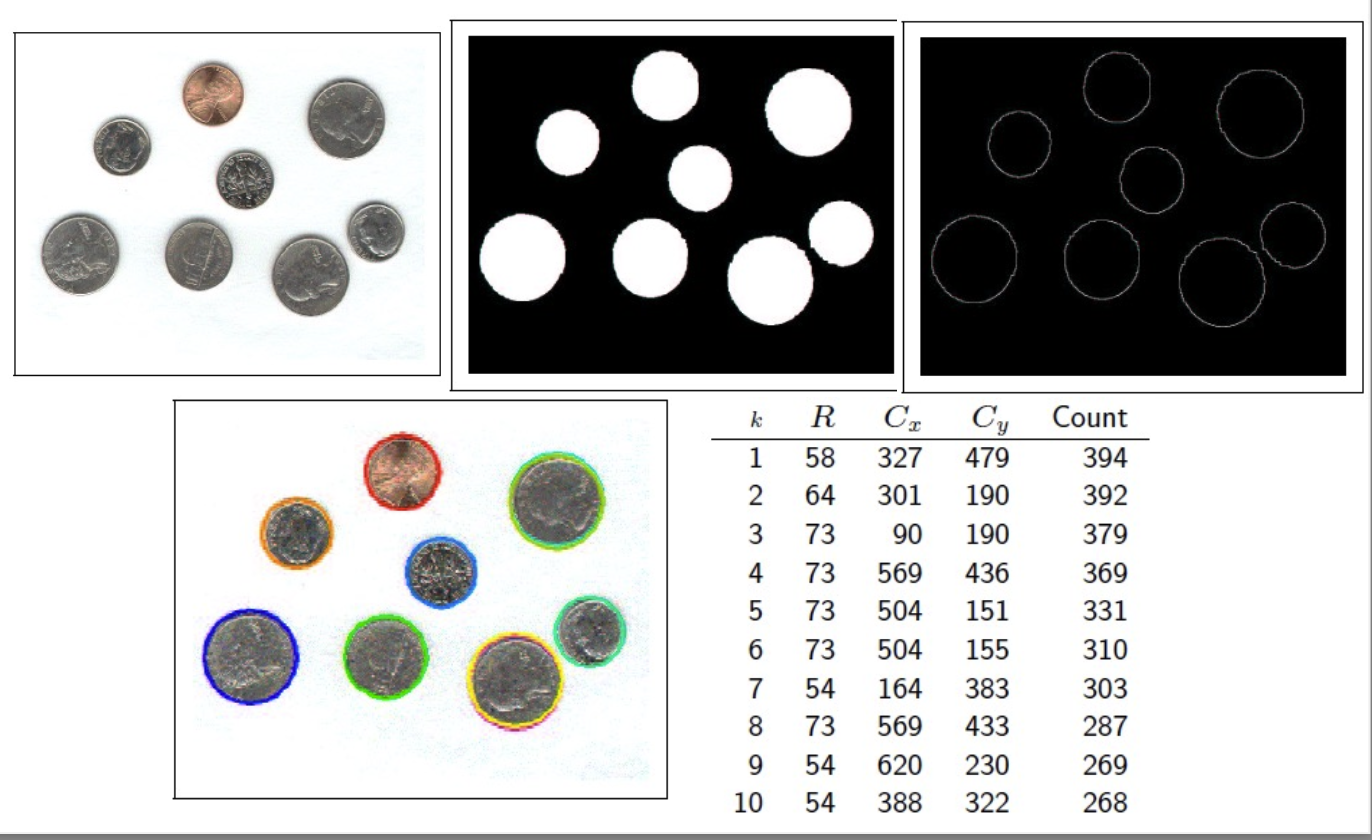
Circle Hough Transform 圓霍夫轉換​

12

Example of Circle Hough Transform 圓霍夫轉換的例子​

13