Skip to main content

Optimization Problems and Local Search Algorithms 優化問題和局部搜索算法

Travelling salesman problem (TSP) 旅行商問題（TSP）​

  • Given: a list of cities and the distances between each pair of them, 給定：城市列表和每對城市之間的距離，
  • Sought: the shortest route that visits each city exactly once and returns to the origin city (the starting point), 找到：訪問每個城市一次並返回起始城市的最短路線，

1

True TSP example 真實 TSP 例子​

Optimal solution for "usa13509" from TSPLIB. Cities with population at least 500 in the continental US (in 1995). In total 13509 cities. 來自 TSPLIB 的 "usa13509" 的最佳解決方案。美國大陸人口至少 500 人的城市（1995 年）。共有 13509 個城市。

Kaggle: Traveling Santa 2018 旅行聖誕老人 2018​

Optimal solution for Kaggle Traveling Santa 2018.

Travelling salesman problem (TSP) 旅行商問題（TSP）​

  • Mentioned in a travelling salesman handbook in 1832 1832 年旅行推銷員手冊中提到
  • Formally defined by the Irish mathematician William. R. Hamilton 愛爾蘭數學家 William. R. Hamilton 正式定義
  • One of the most prominent and widely studied combinatorial optimisation problems in computer science and operations research 最突出和廣泛研究的計算機科學和操作研究中的最突出和廣泛研究的組合優化問題之一
  • Many optimisation problems, e.g., Printed Circuit Boards (PSB) design can be formulated as TSP or its variations 许多优化问题，例如 Printed Circuit Boards（PSB）设计可以被公式化为 TSP 或其变体
  • Conceptually simple but computationally difficult: best benchmark for development and evaluation of combinatorial optimisation algorithms 概念上簡單但計算上困難：最佳基準為組合優化算法的開發和評估

What is optimisation problem? 優化問題是什麼？​

  • Optimization: to find the best or optimal solution to a problem 優化：找到問題的最佳或最佳解決方案
  • Examples are everywhere: 例子無處不在：
    • Portfolio optimisation: you have an investment portfolio, e.g., cash and shares, you know the potential return and financial risk of each asset. How to build the perfect investment portfolio to maximise the return while keep risk in control? 投資組合優化：您有一個投資組合，例如現金和股票，您知道每項資產的潛在回報和財務風險。如何構建完美的投資組合，在風險可控的情況下實現收益最大化？
    • Engineering optimisation: you are required to design a product with some materials. How to design a product with minimal materials while keeping the quality? 工程優化：您需要使用某些材料來設計產品。如何設計一個產品，使用最少的材料，而保持質量？

Definition of optimisation 優化的定義​

  • Definition: 定義：
    • Given: a function f (x) : A → R from some set A to the real numbers 給定：函數 f (x) : A → R 從某個集合 A 到實數
    • Sought: an element x∗ in A such that f (x∗) ≤ f (x) ("minimisation") or f (x∗) ≥ f (x) ("maximisation") for all x in A. 找到：一個元素 x∗ 在 A 中，使得 f (x∗) ≤ f (x)（"最小化"）或 f (x∗) ≥ f (x)（"最大化"）對於所有 x 在 A 中。
  • Function f (x ) is called objective function, or cost function (minimisation), fitness function (maximisation and in Evolutionary Computation) 函數 f (x) 稱為目標函數，或成本函數（最小化），適應度函數（最大化和進化計算）
  • A is called feasible set, which is some subset of the Euclidean space specified by a set of constraints A 稱為可行集，它是由一組約束條件指定的歐幾里得空間的一個子集
  • The domain A of f (x) is called the search space, while the elements of A, e.g., x ∈ A are called candidate solutions or feasible solutions. f (x) 的域 A 稱為搜索空間，而 A 的元素，例如 x∈A 稱為候選解或可行解。

2

Categories of optimisation problems 優化問題的類別​

  • Depends on the nature of objective function: 取決於目標函數的性質：
    • Linear vs non-linear 線性與非線性
    • Linear function: 線性函數：
      • Additivity: f(x+y)=f(x)+f(y)f(x+y) = f(x)+f(y)
      • Homogeneity: f(αx)=αf(x)f(\alpha x) = αf(x) for all α\alpha
    • If it is non-linear: 如果它是非線性的：
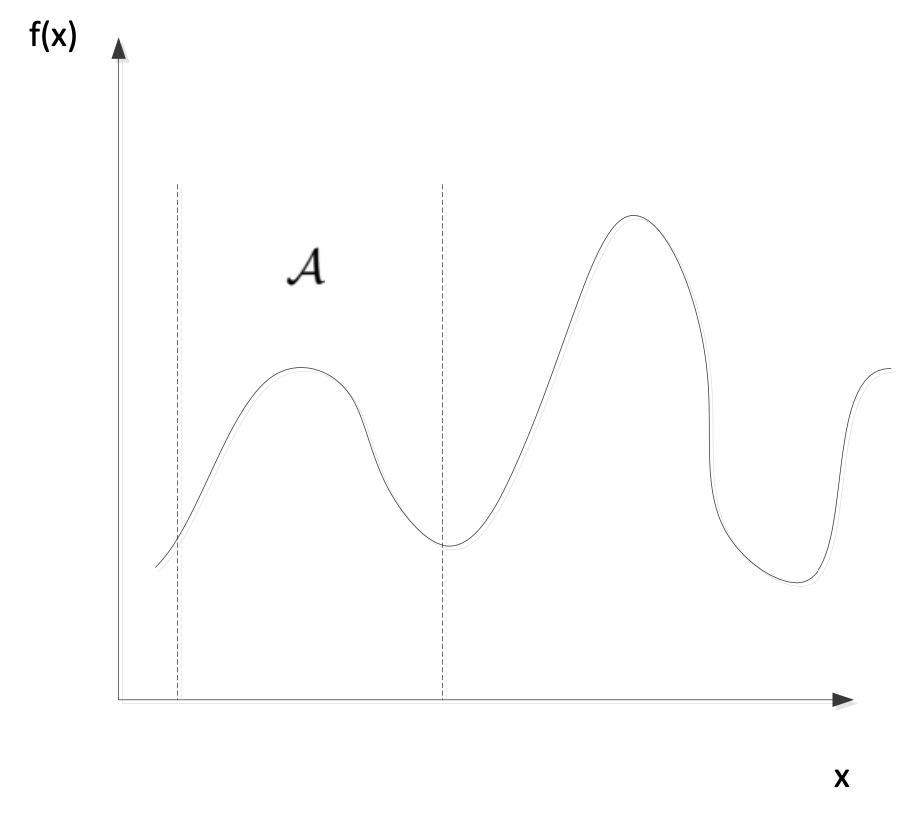
      • Convex vs non-convex 凸與非凸
      • Question: which is more difficult? 題：哪個更困難？
    • Multi-objective vs single objective 多目標與單目標
    • Constrained vs non-constrained 約束與非約束
  • Depends on the nature of solutions: 取決於解決方案的性質：
    • Continuous vs Discrete (also known as a combinatorial optimization) 連續與離散（也稱為組合優化）

Optimisation algorithms 優化算法​

  • Mathematical programming algorithms, e.g., linear programming 數學規划算法，例如線性規劃
  • Search and enumeration algorithms 搜索和枚舉算法
    • Brute force algorithms, enumerating all possible candidate solutions and check 蠻力算法，枚舉所有可能的候選解決方案並檢查
    • Improved brute force algorithms, e.g., branch and bound algorithms 改進的蠻力算法，例如分支界限算法
    • Heuristic algorithms 启发式算法
      • Randomised algorithms 隨機算法
      • Local search, e.g., greedy search 局部搜索，例如貪婪搜索

Solving TSP 解決 TSP​

  • Question 1: What kind of optimisation problem is TSP? TSP 是什麼類型的優化問題？

  • Question 2: What algorithm you can use to solve TSP? 您可以使用哪種算法來解決 TSP？

  • Answer to Question 2: Solve TSP using:

Why heuristic algorithms for TSP? 為什麼 TSP 使用啟發式算法？​

  • TSP is difficult for other algorithms TSP 難於其他算法
    • Brute force algorithms: complexity is O(n!), the factorial of the number of cities. 蠻力算法：複雜度為 O(n!)，城市數量的階乘。
    • Improved brute force algorithms, e.g., branch and cut algorithms: O(1.9999n)O(1.9999^n) [1]
      • Still time consuming, e.g., for usa13509, the running time required is 213509
      • In fact, usa13509 was solved in 1998 by Rice University using two clusters of 44 CPUs, took approximately three months from start to finish (see News)
      • The largest instance of TSP problem is an instance in TSPLIB of 85,900 cities, taking over 136 CPU-years! [2]
    • Linear programming: essentially an integer linear programming problem, itself is a NP-hard problem (See Why LP cannot solve large instances of NP-complete problems in polynomial time)

Randomised algorithms 隨機算法​

  • Two categories of randomised algorithms: 隨機算法的兩個類別：

    • Using random numbers to help find a solution to a problem 使用隨機數幫助找到問題的解決方案
    • Using random numbers to improve a solution to a problem 使用隨機數來改善問題的解決方案

  • For the first category, two representative simple algorithms: 第一類別的兩個代表性簡單算法：

    • Las Vegas algorithm Monte Carlo algorithm 莱斯維加斯算法蒙特卡羅算法

  • Question: how to use Monte Carlo or Les Vegas to solve TSP? Or more specifically, how to generate random solutions to TSP? 如何使用蒙特卡羅或莱斯維加斯來解決 TSP？或更具體地說，如何生成 TSP 的隨機解決方案？

  • Observation: Randomised search algorithms such as Monte Carlo or Les Vegas return bad results for TSP. 隨機搜索算法，如蒙特卡羅或莱斯維加斯，對 TSP 返回了不好的結果。

  • Question: Why randomised search algorithms cannot solve TSP? 為什麼隨機搜索算法無法解決 TSP？

Local search algorithms 局部搜索算法​

  • Local search: a heuristic algorithm for solving hard optimization problems 局部搜索：用於解決嚴重優化問題的啟發式算法
    • Idea: start with an initial guess at a solution and incrementally improve it until it is one 想法：從對解決方案的初步猜測開始，逐步改進它直到它成為一個解決方案
    • Incremental improvement: local changes, e.g., the algorithm iteratively moves to a neighbour solution 增量改進：局部變化，例如，算法迭代地移動到鄰居解決方案
    • Neighbour solution: Depends on the definition of a neighbourhood relation on the search space, but generally based on similarity (distance) measure 鄰居解決方案：取決於搜索空間上鄰居關係的定義，但通常基於相似性（距離）度量

Generic local search algorithm 通用局部搜索算法​

3

Note: termination criterion could be maximum iteration is reached or no improvement for a certain iterations. 終止條件可以是達到最大迭代次數或某些迭代次數沒有改善。

Hill climbing algorithm 山爬算法​

  • One of the simplest local search algorithms 一個最簡單的局部搜索算法
  • Hill climbing is an algorithm that more like "climbing Everest in thick fog with amnesia" 山爬算法是一種更像是"在濃霧中失憶的爬上珠穆朗瑪峰"一樣的算法
  • An iterative algorithm: 一個迭代算法：
    • Starts with an arbitrary solution to a problem, 從問題的任意解決方案開始，
    • Iteratively searches a better solution from the current solution's immediate neighbour solutions 迭代地從當前解決方案的鄰居解決方案中搜索更好的解決方案
    • Immediate neighbour solutions: most similar solutions to the current solution. 與當前解決方案最相似的解決方案。
  • Two types of hill climbing: 兩種山爬算法：
    • Simple hill climbing: chooses the first better solution 簡單爬山：選擇第一個更好的解決方案
    • Steepest ascent hill climbing: compares all neighbour solutions and chooses the best solution 最陡的上升爬山：比較所有鄰居解決方案並選擇最好的解決方案

Simple hill climbing algorithm 簡單爬山算法​

4

Hill climbing for TSP problem TSP 问题的山爬算法​

  • Question: How to construct the immediate neighbour solutions of the current solution for TSP? 如何為 TSP 構造當前解決方案的鄰居解決方案？

Let's take a look at some simple examples 讓我們看一些簡單的例子​

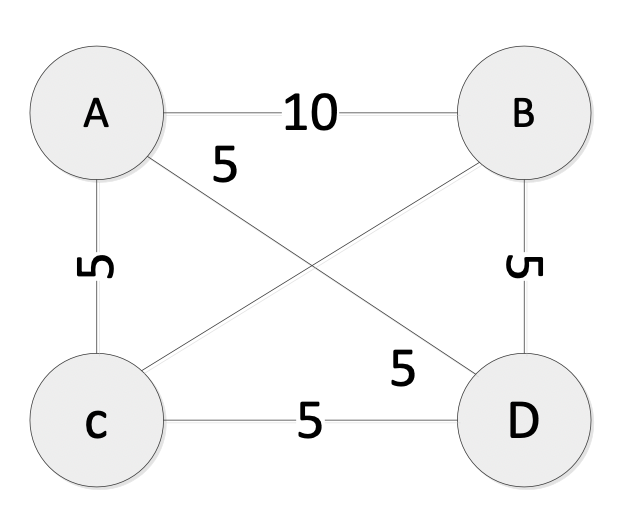
  • 2-3 cities: only one solutions 2-3 城市：只有一個解決方案
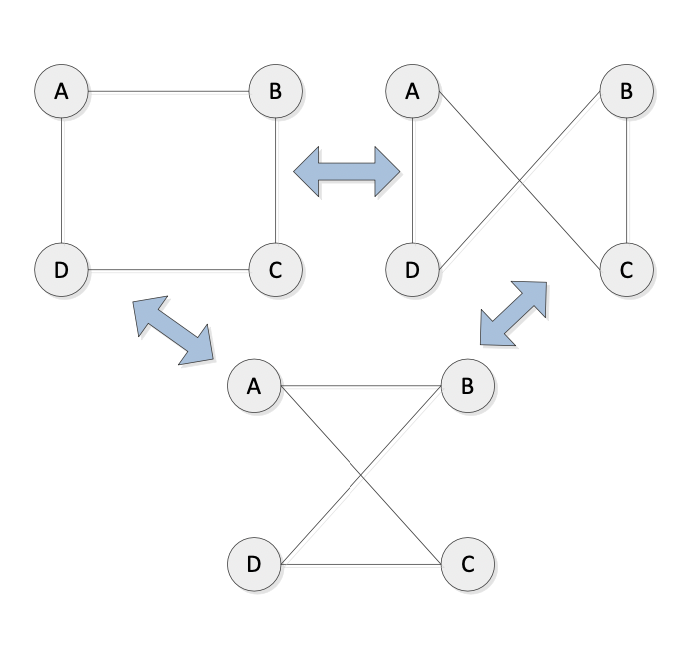
  • 4 cities: 3 solutions 4 城市：3 個解決方案
  • Question: How those tours of the 4 cities TSP differ? 這些 4 城市 TSP 的旅行路線有什麼不同？

5

Conclusion 結論​

  • Optimisation problems can be very difficult 優化問題可能非常困難
  • Some of them are NP-hard: exact optimal solution of NP-problems requires (in the worst case) an exhaustive search. 有些問題是 NP-困難的：NP 問題的精確最佳解決方案需要（在最壞情況下）一個完整的搜索。
  • Heuristic algorithms are useful for difficult optimisation problems 啟發式算法對於困難的優化問題很有用
  • Optimisation is all about exploration and exploitation 優化是探索和開發的一切
  • Randomness can facilitate exploration, but not exploitation (local search) 隨機性可以促進探索，但不能促進開發（局部搜索）

[1]: Woeginger, G.J. (2003), "Exact Algorithms for NP-Hard Problems: A Survey", Combinatorial Optimization – Eureka, You Shrink! Lecture notes in computer science, vol. 2570, Springer, pp. 185–207.

[2] Applegate, D. L.; Bixby, R. M.; Chv ́atal, V.; Cook, W. J. (2006), The Traveling Salesman Problem, ISBN 0-691-12993-2.