递归函数 Recursive Functions
这些笔记应该与我们的教科书《Haskell 编程》的第 6 章结合起来阅读。
We discuss some examples from the Haskell'98 standard prelude for pedagogical purposes.
See the prelude for the current version of the language for all predefined classes and their instances.
基本概念
There is also a video on this section.
正如我们所看到的,许多函数可以很自然地用其他函数来定义。例如,一个返回非负整数阶乘的函数可以通过使用库函数计算 1 与给定数之间的整数的乘积来定义:
fac :: Int -> Int
fac n = product [1..n]
表达式的评估是通过对其参数应用函数的逐步过程进行的。
For example:
fac 5
= product [1..5]
= product [1,2,3,4,5]
= 1*2*3*4*5
= 120
在 Haskell 中,函数也可以用自身来定义。这样的函数被称为递归。
fac :: Int -> Int
fac 0 = 1
fac n = n * fac (n-1)
函数 fac 将 0 映射为 1(base case),将任何其他整数映射为其本身与其前身的阶乘的积(recursive case)。
For example:
fac 3
= 3 * fac 2
= 3 * (2 * fac 1)
= 3 * (2 * (1 * fac 0))
= 3 * (2 * (1 * 1))
= 3 * (2 * 1)
= 3 * 2
= 6
Note:
fac 0 = 1 is appropriate because 1 is the identity for multiplication: 1 x = x = x 1.
递归定义在整数<0 的情况下出现分歧,因为永远不会达到基数:
> fac (-1)
*** Exception: stack overflow
递归为什么有用? Why is Recursion Useful?
有些函数,如阶乘,用其他函数来定义比较简单。
然而,正如我们将看到的那样,许多函数可以自然而然地以自身为单位进行定义。
使用递归定义的函数的属性可以用简单但强大的数学技术归纳法来证明。
列表上的递归 Recursion on Lists
There is also a video on this section.
递归并不限于数字,也可以用来定义列表上的函数。
product' :: Num a => [a] -> a
product' [] = 1
product' (n:ns) = n * product' ns
product' 函数将空列表映射为 1(base case),任何非空列表映射为其头部乘以其尾部的 product'(recursive case)。
For example:
product' [2,3,4]
= 2 * product' [3,4]
= 2 * (3 * product' [4])
= 2 * (3 * (4 * product' []))
= 2 * (3 * (4 * 1))
= 24
注意:Haskell 中的列表实际上是使用 cons 操作符一次构建一个元素。因此,[2,3,4] 只是 2:(3:(4:[])的一个缩写。)
使用与 product' 相同的递归模式,我们可以在列表中定义长度函数。
length :: [a] -> Int
length [] = 0
length (_:xs) = 1 + length xs
length 函数将空列表映射为 0(base case),将任何非空列表映射为其尾部长度的继承者(recursive case)。
For example:
length [1,2,3]
= 1 + length [2,3]
= 1 + (1 + length [3])
= 1 + (1 + (1 + length []))
= 1 + (1 + (1 + 0))
= 3
使用类似的递归模式,我们可以在列表上定义反向函数。
reverse :: [a] -> [a]
reverse [] = []
reverse (x:xs) = reverse xs ++ [x]
函数 reverse 将空列表映射为空列表,将任何非空列表映射为其尾部附加在头部的反向。
For example:
reverse [1,2,3]
= reverse [2,3] ++ [1]
= (reverse [3] ++ [2]) ++ [1]
= ((reverse [] ++ [3]) ++ [2]) ++ [1]
= (([] ++ [3]) ++ [2]) ++ [1]
= [3,2,1]
有趣的是,上例中使用的 append opearator ++ 也可以用递归来定义。
(++) :: [a] -> [a] -> [a]
[] ++ ys = ys
(x:xs) ++ ys = x : (xs ++ ys)
For example:
[1,2,3] ++ [4,5]
= 1 : ([2,3] ++ [4,5])
= 1 : (2 : ([3] ++ [4,5]))
= 1 : (2 : (3 : ([] ++ [4,5])))
= 1 : (2 : (3 : [4,5]))
= [1,2,3,4,5]))
++ 的递归定义正式表明了这样一个观点:两个列表可以通过从第一个列表中复制元素来追加,直到它被耗尽,这时第二个列表就会被加入到最后。
多个论据 Multiple Arguments
There is also a video on this section.
有一个以上参数的函数也可以用递归来定义。
- 对两个列表的元素进行压缩:
zip :: [a] -> [b] -> [(a,b)]
zip [] _ = []
zip _ [] = []
zip (x:xs) (y:ys) = (x,y) : zip xs ys
For example:
zip ['a', 'b', 'c'] [1,2,3,4]
= ('a',1) : zip ['b', 'c'] [2,3,4]
= ('a',1) : ('b',2) : zip ['c'] [3,4]
= ('a',1) : ('b',2) : ('c',3) : zip [] [4]
= ('a',1) : ('b',2) : ('c',3) : []
= [('a',1), ('b',2), ('c',3)]
- 从一个列表中删除前 n 个元素:
drop :: Int -> [a] -> [a]
drop 0 xs = xs
drop _ [] = []
drop n (_:xs) = drop (n-1) xs
For example:
drop 3 [4,6,8,10,12]
= drop 2 [6,8,10,12]
= drop 1 [8,10,12]
= drop 0 [10,12]
[10,12]
多重递归 Multiple Recursion
There is also a video on this section.
函数也可以用 mulitple recursion 来定义,即一个函数在它自己的定义中被应用不止一次。
一个计算任何整数 n >= 0 的第 n 个斐波那契数(0, 1, 1, 2, 3, 5, 8, 13, ...)的函数可以用双递归定义如下:
fib :: Int -> Int
fib 0 = 0
fib 1 = 1
fib n = fib (n-2) + fib (n-1)
For example:
fib 4
= fib (2) + fib (3)
= fib (0) + fib (1) + fib (1) + fib (2)
= 0 + 1 + 1 + fib (0) + fib (1)
= 0 + 1 + 1 + 0 + 1
= 3
相互递归 Mutual Recursion
There is also a video on this section.
函数也可以用相互递归来定义,即两个或多个函数相互递归地定义。对于非负整数,我们可以使用相互递归来定义偶数和奇数。
even :: Int -> Bool
even 0 = True
even n = odd (n-1)
odd :: Int -> Bool
odd 0 = False
odd n = even (n-1)
For example:
even 4
= odd 3
= even 2
= odd 1
= even 0
= True
同样,从一个列表的所有偶数和奇数位置(从零开始计算)选择元素的函数可以定义如下。
evens :: [a] -> [a]
evens [] = []
evens (x:xs) = x : odds xs
odds :: [a] -> [a]
odds [] = []
odds (_:xs) = evens xs
For example:
evens "abcde"
= 'a' : odds "bcde"
= 'a' : evens "cde"
= 'a' : 'c' : odds "de"
= 'a' : 'c' : evens "e"
= 'a' : 'c' : 'e' : odds []
= 'a' : 'c' : 'e' : []
= "ace"
编程实例 Programming Example - Quicksort
There is also a video on this section.
对一个数值列表进行排序的 quicksort 算法可以由以下两条规则指定。
空列表已经被排序
非空列表可以通过对尾部值 <= 头部进行排序,对尾部值 > 头部进行排序,然后将得到的列表附加在头部值的两侧。
使用递归,这个规范可以直接转化为一个实现。
qsort :: Ord a => [a] -> [a]
qsort [] = []
qsort (x:xs) = qsort smaller ++ [x] ++ qsort larger
where
smaller = [a | a <- xs, a <= x]
larger = [b | b <- xs, b > x]
注意:这可能是任何编程语言中最简单的 quicksort 的实现了。
For example (abbreviating qsort as q):
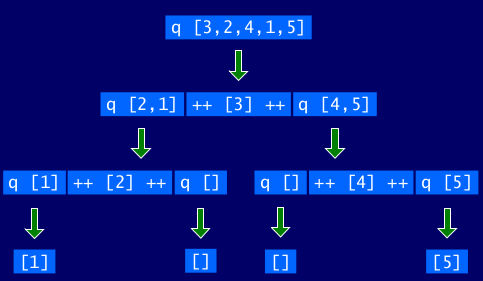
关于递归的建议
There is also a video on this section.
在这一节中,我们为定义一般的函数,特别是递归函数提供一些建议,使用五步程序。
Example - drop: that removes a given number of elements from the start a list.
- Step 1: 定义类型
drop 函数接收一个整数和一个某种类型的值的列表 a,并产生另一个这种值的列表。
drop :: Int -> [a] -> [a]
在定义这一类型时,我们已经做出了四个设计决定:
(i) using integers rather than a more general numeric type - for simiplicity
(ii) using currying rather than taking arguments as a pair - for flexibility
(iii) supplying the integer argument before the list argument - for readability (drop n elements from xs)
(iv) making the function polymorphic in the type of the list elements - for generality.
- Step 2: enumerate the cases
我们总共有四种可能的情况,即整数参数有两种可能的值(0 和 n),列表参数有两种可能([]和(x:xs)),因此我们有四种可能的组合(情况)。
drop 0 [] =
drop 0 (x:xs) =
drop n [] =
drop n (x:xs) =
- Step 3: 定义简单的情况
根据定义,从任何列表的开头去除 0 个元素都会得到相同的列表。
drop 0 [] = []
drop 0 (x:xs) = x:xs
drop n [] =
drop n (x:xs) =
试图从空列表中删除一个或多个元素是无效的,所以第三种情况可以省略,如果出现这种情况,就会产生一个错误。然而,我们选择在这种情况下通过返回空列表来避免错误的产生:
drop 0 [] = []
drop 0 (x:xs) = x:xs
drop n [] = []
drop n (x:xs) =
- Step 4: define the other cases
对于从一个非空列表中删除一个或多个元素,我们放弃列表的头部,并递归调用自身,比之前在列表尾部的调用少一个。
drop 0 [] = []
drop 0 (x:xs) = x:xs
drop n [] = []
drop n (x:xs) = drop (n-1) xs
- Step 5: 概括和简化
关于放弃的前两个方程可以合并为一个单一的方程,即从任何列表中移除零元素都会得到相同的列表:
drop 0 xs = xs
drop n [] = []
drop n (x:xs) = drop (n-1) xs
第二个方程中的变量 n 和第三个方程中的 x 可以用通配符模式 _ 代替,因为这些变量没有在其方程的主体中使用。
drop :: Int -> [a] -> [a]
drop 0 xs = xs
drop _ [] = []
drop n (_:xs) = drop (n-1) xs
这恰恰是在标准的 Prelude 中可用的 drop 函数的定义。
练习
(1) 不看标准序言,用递归定义以下库函数。
- 决定一个列表中的所有逻辑值是否为真:
and :: [Bool] -> Bool
答案
and :: [Bool] -> Bool
and [] = False
and (x:xs) = x && (and xs)
- 串联一个列表:
concat :: [[a]] -> [a]
答案
concat :: [[a]] -> [a]
concat [] = []
concat (x:xs) = x ++ concat xs
- 生成一个有 n 个相同元素的列表:
replicate :: Int -> a -> [a]
答案
replicate :: Int -> a -> [a]
replicate n x | n <= 0 = []
| otherwise = x : replicate (n-1) x
- 选择一个列表中的第 n 个元素:
(!!) :: [a] -> Int -> a
答案
(!!) :: [a] -> Int -> a
(!!) [] _ = undefined
(!!) (x:xs) n | n == 0 = x
| otherwise = (!!) xs (n-1)
- 决定一个值是否是一个列表的元素:
elem :: Eq a => a -> [a] -> Bool
答案
elem :: Eq a => a -> [a] -> Bool
elem n [] = False
elem n (x:xs) | x == n = True
| otherwise = elem n xs
(2) 定义一个递归函数
merge :: Ord a => [a] -> [a] -> [a]
合并两个排序的数值列表,得到一个单一的排序列表。
For example:
> merge [2,5,6] [1,3,4]
[1,2,3,4,5,6]
答案
merge :: Ord a => [a] -> [a] -> [a]
merge x [] = x
merge [] y = y
merge (x:xs) (y:ys) | x <= y = x:(merge xs (y:ys))
| otherwise = y:(merge (x:xs) ys)